Comphy

Cryogenic Charge Trapping

The WKB approximation to the quantum mechanical NMP model

The classical approximation of the 2-state NMP model is well suited for describing charge transfer processes above room temperature. However, it breaks down at cryogenic temperatures since it predicts a total freeze out of charge transitions, while multiple studies have shown active charge trapping at cryogenic temperatures.

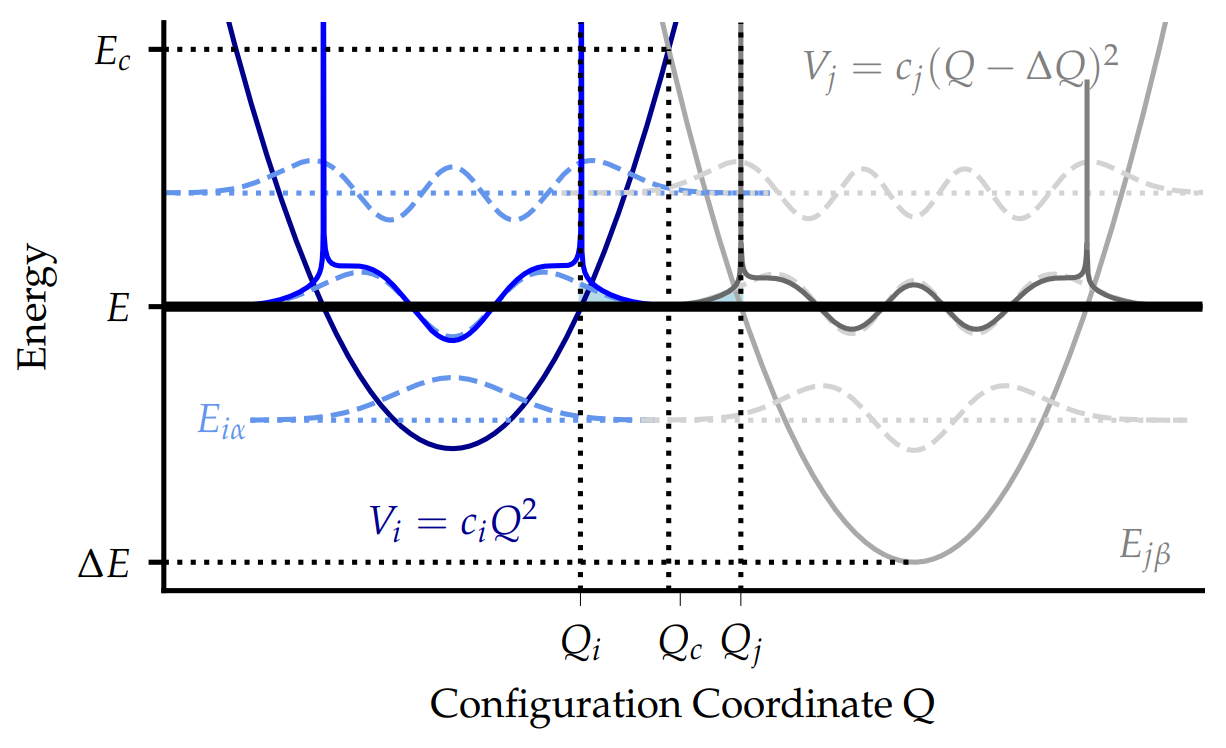
In principle it would be necessary to use the full quantum mechanical version of the 2-state NMP model for cryogenic modeling. However, the computation of the full quantum mechanical transition rates is numerically expensive, because it requires to compute the eigenstates of the potential energy surfaces and the corresponding overlap functions. One approach to solving this issue is to replace the vibrational wave functions of the full quantum mechanical 2-state NMP model by their respective Wentzel-Krammer-Brillouin (WKB) approximations, as shown in Fig. 1:

comphy-band_diagram_traps — The vibrational wave functions (dashed) of the potential energy curves representing the neutral and charged states can be approximated using WKB-based wave functions (solid). The overlap of the wavefunctions is dominated by their exponentially decaying parts which allows the formulation of a simplified expression for the charge transition rates.

At cryogenic temperatures, the overlap integrals are dominated by the exponentially decaying part of the WKB wave functions, which allows to approximate the overlap integral analytically. The transition rate \( k_{ij} \) then evaluates to: \begin{equation} k_{ij}(T) = C(E^*)\exp\left(\frac{-E^*}{k_\mathrm{B}T}+\varphi(E^*)\right)\sqrt{\frac{2\pi}{\varphi''(E^*)}} \end{equation} where the energy \( E^* \) is given by the implicit relation: \begin{equation} \frac{\mathrm{d}\varphi(E)}{\mathrm{d}E}\bigg\rvert_{E=E^*}=\frac{1}{k_\mathrm{B}T} \end{equation} This approach gives very similar results as the full quantum mechanical model while being computationally much more efficient. However, Eq. 2 can only be solved numerically. Consequently, this approach still lags behind the classical approximation in terms of speed.

For further numerical improvement a model based on the assumption of linear coupling \( (𝑅 = 1) \) was implemented in Comphy. For \(𝑅 = 1\), the curvatures of the vibrational wave functions do not change upon charge trapping, implying that the effective phonon frequencies are also the same in both defect charge states \( ( \omega_i=\omega_j=\omega) \). In this case, it is possible to use an analytic expression for the quantum mechanical transition rates in the strong electron-phonon coupling regime at cryogenic temperatures. This approach leads to the following transition rates \( k_{ij} \): \begin{equation} \begin{aligned} k_{ij}(T) = \omega \frac{\sqrt{2\pi}}{2D\hbar} \bigg[ & (1 + \coth \alpha) \exp \left( \frac{-E_\mathrm{-}}{2D^2\hbar^2} \right) \\ & - (1 - \coth \alpha) \exp \left( \frac{-E_\mathrm{+}}{2D^2\hbar^2} \right) \bigg] \end{aligned} \end{equation} with the abbreviations \( D = \sqrt{ \omega E_\mathrm{R} (2n+1)/\hbar} \), \( n = 1/(\exp(\hbar \omega/k_\mathrm{B}T)-1) \), \( \alpha=\hbar\omega/2k_\mathrm{B}T \), \( E_{\pm} = \Delta E \pm \hbar \omega - E_\mathrm{R} \) and \( \omega = \sqrt{ 2 E_\mathrm{R}} / \Delta Q \).

This closed form expression for linear coupling gives the same results as the full quantum mechanical model over a wide temperature range, but its evaluation requires a comparable computational effort as the classical approximation. Thus, it is well suited for efficient reliability simulations with thousands of defects in a device.

This section was a brief summary of the publication D. Waldhoer et al. "Comphy v3.0 -- A Compact-Physics Framework for Modeling Charge Trapping Related Reliability Phenomena in MOS Devices". An in-depth description of the employed models can be found in the related publication J. Michl et al. "Efficient Modeling of Charge Trapping at Cryogenic Temperatures—Part I: Theory". In order to gain a more detailed understanding of the application of the WKB approximation to the quantum mechanical NMP model we encourage you to read both papers.

Performing a cryogenic BTI simulation

For the computation of BTI at cryogenic temperatures it is necessary to use the quantum mechanical trapbands TrapBand_2S_NMP_QM instead of the classical trapbands TrapBand_2S_NMP during the device setup. The quantum-mechanical trap bands can be initialized in a completely analogous way to the classical ones, but require an additional parameter dQ, called the shift in the configuration coordinate. The parameter dQ essentially determines the rate at which charge trapping becomes increasingly unlikely towards cryogenic temperatures:

grid_sampler = GaussianGridSampler(

dx=1.0E-10,	# grid spacing for sampling xt in m
dEt=0.05,	# grid spacing for sampling of Et in eV
dEr=0.1,	# grid spacing for sampling of Er in eV
non_coverage=1.0E-4,	# sets boundary of gaussian grid

)

SiO2_shallow_trap_band = TrapBand_2S_NMP_QM(

x_start=0.0E-9,	# lower bound of spatial defect distribution in m
x_end=1.0E-9,	# upper bound of spatial defect distribution in m
Et=-3.51,	# mean energy level in eV
Et_sigma=0.01,	# standard dev. of energy level in eV
Er=1.5,	# mean relaxation energy in eV
Er_sigma=0.2,	# standard dev. of relaxation energy in eV
R=1.001,	# curvature ratio
Nt=1.5E25,	# defect concentration in m⁻³
trap_type='donor',	# type of traps
sampler=grid_sampler,	# a appropriate grid sampler
device=my_device,	# the device to which you want to add the traps
dQ=3.0,	# configuration coordinate

)
my_device.trap_bands['SiO2_deep_trap_band'] = SiO2_deep_trap_band

The (approximation) mode of the simulation can be selected at device initialization:

my_device.initialize(Vg=Vg[0], T=temperature[0], transition_mode='wkb', savebands=False)

The transition mode can be either set to ‘WKB’ or ‘R=1’. If ‘WKB’ is selected the exact vibrational wave functions are replaced by their respective WKB-approximations, during the calculation of the quantum mechanical NMP transition rates. If ‘R=1’ is selected, the closed form expression for linear coupling, which is only valid for a curvature ratio close to 1, is used instead. As emphasized above the latter option leads to a considerable speed-up of the simulation.

The new quantum mechanical trapbands allow to perform BTI simulations analogously to the classical trap bands, but at cryogenic temperatures. Note that the calculation of the device electrostatics may suffer from numerical problems at very low temperatures and therefore may not be very accurate at these temperatures.
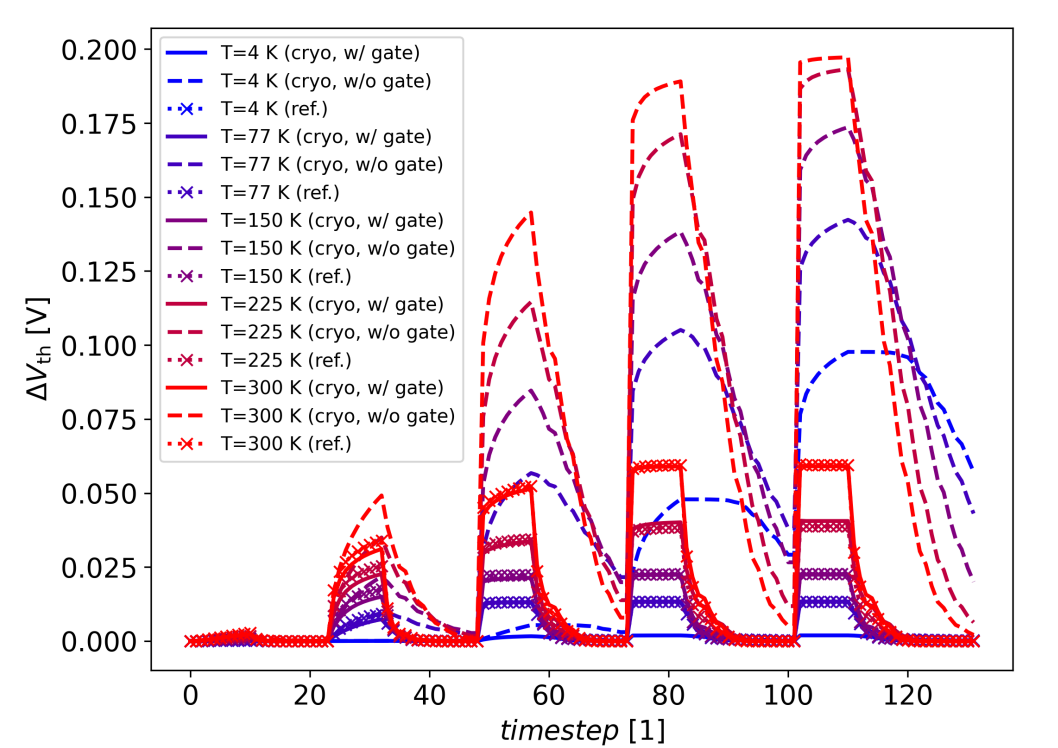
For example Fig. 2 shows a comparison of a BTI simulation performed with classical and quantum mechanical trap bands. The results show that the classical reference freezes out completely, while the cryogenic rates allow for some charge trapping even at 4K. It should be noted that turning on gate interaction can have a drastic impact on trapping kinetics and therefore usually requires re-calibration of the defect bands across all temperatures.